算法学习：bfs+dfs

–

概念

深度优先搜索算法（Depth-First-Search），是搜索算法的一种。它沿着树的深度遍历树的节点，尽可能深的搜索树的分 支。堆栈实现，递归实现

广度优先搜索算法（Breadth-First-Search），是一种图形搜索算法，从根节点开始，沿着树(图)的宽度遍历树(图)的节点。队列实现

–

机器人的运动范围

地上有一个m行n列的方格，从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动，它每次可以向左、右、上、下移动一格（不能移动到方格外），也不能进入行坐标和列坐标的数位之和大于k的格子。例如，当k为18时，机器人能够进入方格 [35, 37] ，因为3+5+3+7=18。但它不能进入方格 [35, 38]，因为3+5+3+8=19。请问该机器人能够到达多少个格子？

示例 1：

输入：m = 2, n = 3, k = 1
输出：3
示例 2：

输入：m = 3, n = 1, k = 0
输出：1
提示：

1 <= n,m <= 100
0 <= k <= 20

======================================

1. 如何计算行坐标和列坐标的数位之和

对于一个整数 n，我们有以下伪代码模板：

int sum = 0;
    while (n > 0){
        sum += n % 10; // n对10取余
        n /= 10;       // n等于整除10之后的值
    }
    return sum;

因此我们只需将行坐标和列坐标分别求数位之和，将其结果相加即可。

2. 哪些格子在运动范围之内

机器人的运动范围需要同时满足以下两个条件：

• 当前格子坐标数位之和不大于 k；

• 从坐标 (0, 0) 通过上下左右移动可以到达当前格子

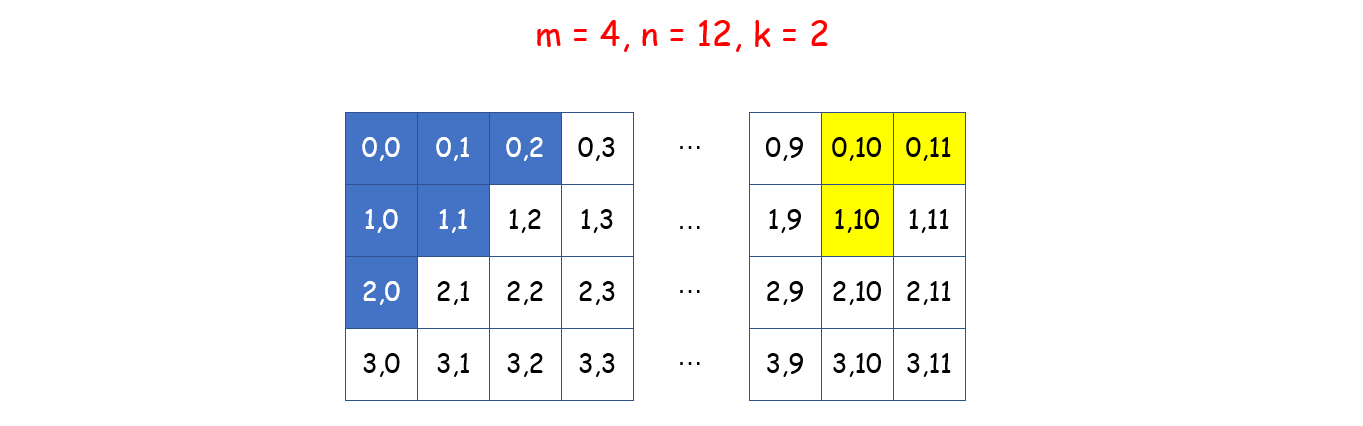
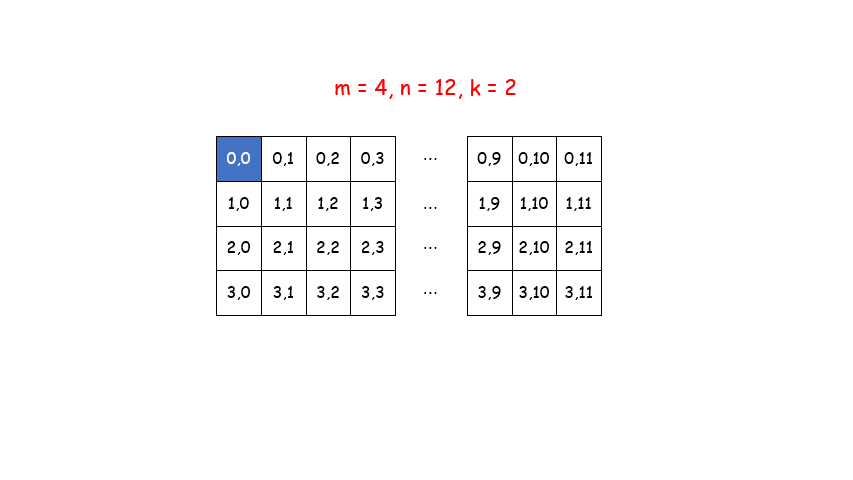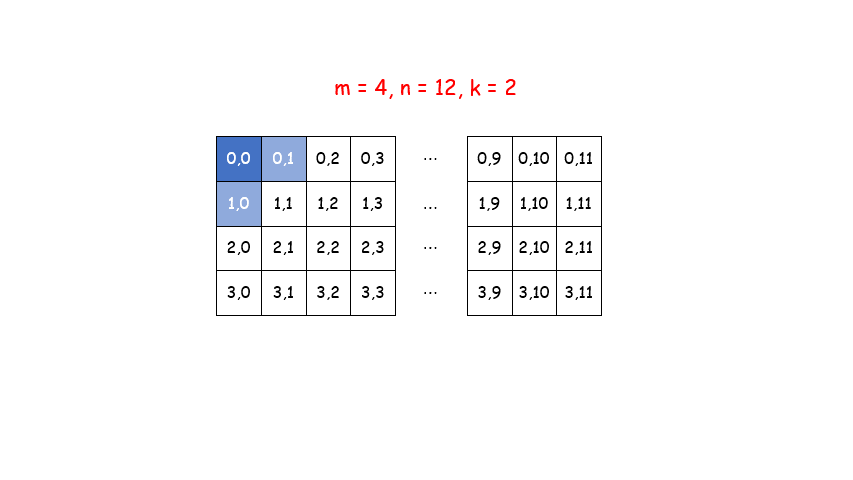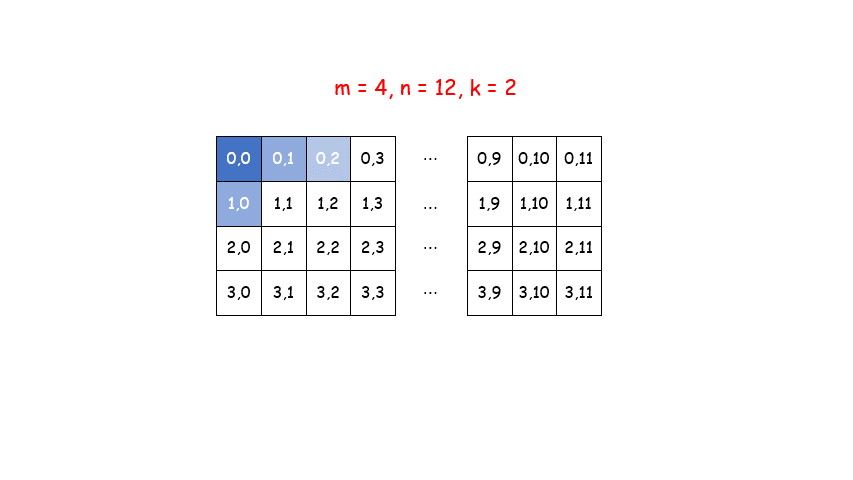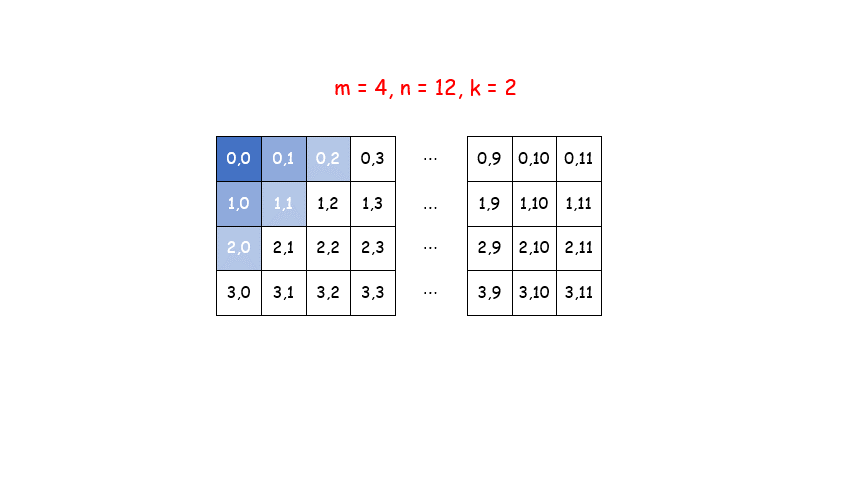
对于上面的矩阵 m = 4, n = 12, k = 2，蓝色区域是满足条件的格子，所以返回结果为 6。需要注意的是，黄色区域虽然满足数位之和不大于 k，但是由于不满足第二个条件，即无法从 (0, 0) 位置移动过去，故不计算在结果之内。

我们可以将矩阵看作一个有向图，而遍历图的方式一般分为广度优先搜索（BFS）和深度优先搜索（DFS），因此从 (0, 0) 点出发，采用 BFS 或 DFS ，如果当前格子满足以上两个条件，则将结果加 1。

方法一：广度优先搜索 BFS

广度优先搜索一般使用队列来实现。我们先将 (0, 0)加入队列，当队列不为空时，每次将队首坐标出队，加入到集合中，再将满足以上两个条件的坐标加入到队尾，直到队列为空。

代码

非常感谢 @tike5 对 BFS 和 DFS 代码提出的优化方法：

在广度优先算法，由于可行解的连通性和结构，仅考虑向下和向右的移动方向即可，深度优先算法同样如此。

由于题目要求从 (0, 0) 点出发，因此任何一个点都可以只通过向右和向下两个动作达到，因此代码中可以只考虑这两个方向。

class Solution:
    def sum_rc(self,row,col):
        tmp = 0
        while row > 0:
            tmp += row % 10
            row //= 10
        while col > 0:
            tmp += col % 10
            col //= 10
        return tmp

    def movingCount(self, m: int, n: int, k: int) -> int:
        marked = set()  # 将访问过的点添加到集合marked中,从(0,0)开始
        queue = collections.deque()
        queue.append((0,0))
        while queue:
            x, y = queue.popleft()
            if (x,y) not in marked and self.sum_rc(x,y) <= k:
                marked.add((x,y)) 
                for dx, dy in [(1,0),(0,1)]:  # 仅考虑向右和向下即可
                    if 0 <= x + dx < m and 0 <= y + dy < n:
                        queue.append((x+dx,y+dy)) 
        return len(marked)

复杂度分析

• 时间复杂度：O(m×n)。

• 空间复杂度：O(m×n)。

方法二：深度优先搜索 DFS

深度优先搜索一般使用栈来实现。本题使用递归可以更轻松实现，我们定义一个递归函数 dfs()，如果坐标不满足条件，结束递归状态，否则将下一步满足条件的坐标代入递归函数。

class Solution:
    def movingCount(self, m: int, n: int, k: int) -> int:
        def sumofDigit(x, y):
            result = 0
            while x > 0:
                result += x % 10
                x //= 10
            while y > 0:
                result += y % 10
                y //= 10
            return result
        
        def dfs(i, j):
            if i == m or j == n or sumofDigit(i, j) > k or (i, j) in marked:
                return 
            marked.add((i, j))
            dfs(i + 1, j)
            dfs(i, j + 1)
            
        marked = set()
        dfs(0, 0)
        return len(marked)

感谢 @ZacBi 对代码可读性提出的建议 🙂

复杂度分析

• 时间复杂度：O(m×n)。

• 空间复杂度：O(m×n)。

作者：z1m

链接：https://leetcode-cn.com/problems/ji-qi-ren-de-yun-dong-fan-wei-lcof/solution/bfs-by-z1m/

来源：力扣（LeetCode）

著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

–

–