目录
-
快速排序的介绍
-
快速排序的Python实现
快速排序的介绍
快速排序(quick sort)的采用了分治的策略。
-
分治策略指的是:
将原问题分解为若干个规模更小但结构与原问题相似的子问题。递归地解这些子问题,然后将这些子问题的解组合为原问题的解。 -
快排的基本思想是:
在序列中找一个划分值,通过一趟排序将未排序的序列排序成 独立的两个部分,其中左边部分序列都比划分值小,右边部分的序列比划分值大,此时划分值的位置已确认,然后再对这两个序列按照同样的方法进行排序,从而达到整个序列都有序的目的。
快速排序的Python实现
先来看一个 我更想称之为伪快排的快排代码:
def quick_sort(array): if len(array) < 2: return array else: pivot = array[0] less_than_pivot = [x for x in array if x <= pivot] more_than_pivot = [x for x in array if x > pivot] return quick_sort(less_than_pivot) + [pivot] + quick_sort(more_than_pivot)
这段代码最关键的是pivot这个参数,这段代码里取序列的第一个元素,然后以这个元素为分组的基准,利用列表解析式使得它左边的值都比它小,右边的值都比它大。然后再分别对这些序列进行递归排序。
这段代码虽然短小利于理解,但是其效率很低,主要体现在以下方面:
-
分组基准的选取过于随便,不一定可以取到列表的中间值
-
空间复杂度大,使用了两个列表解析式,而且每次选取进行比较时需要遍历整个序列。
-
若序列长度过于小(比如只有几个元素),快排效率就不如插入排序了。
-
递归影响性能,最好进行优化。
下面用Python写一个C风格的快排(这里可以体会到快排的精髓):
def quick_sort(L): return q_sort(L, 0, len(L) - 1) def q_sort(L, left, right): if left < right: pivot = Partition(L, left, right) q_sort(L, left, pivot - 1) q_sort(L, pivot + 1, right) return L def Partition(L, left, right): pivotkey = L[left] while left < right: while left < right and L[right] >= pivotkey: right -= 1 L[left] = L[right] while left < right and L[left] <= pivotkey: left += 1 L[right] = L[left] L[left] = pivotkey return left L = [5, 9, 1, 11, 6, 7, 2, 4] print(quick_sort(L))
快速排序需要提供三个参数:待排序序列 、序列最小下标值left、序列最大下标值right。让用户提供这三个参数很麻烦。这里写个函数进行封装:
def quick_sort(L): return q_sort(L, 0, len(L) - 1)
下面看一下q_sort函数:
def q_sort(L, left, right): if left < right: pivot = Partition(L, left, right) q_sort(L, left, pivot - 1) q_sort(L, pivot + 1, right) return L
这个函数的核心是pivot = Partition(L, left, right),在执行它之前,列表的值为[5, 9, 1, 11, 6, 7, 2, 4],而Partition函数做的事情是找到一个分组标准,然后进行分组,让它左边的值比它小,右边的值比它大。
在经过Partition函数分组后,列表变为[4, 2, 1, 5, 6, 7, 11, 9],并把5的下标值(也就是3)返回给pivot,此时列表变成两个小列表[4, 2, 1]和[5, 6, 7, 11, 9] ,之后调用q_sort,就是调用q_sort(L,0, 2)和q_sort(L, 4 ,7),对其进行Partition操作,直到整个列表有序为止。
下面看看关键的Partition函数是如何做的:
def Partition(L, left, right): pivotkey = L[left] while left < right: while left < right and L[right] >= pivotkey: right -= 1 L[left] = L[right] while left < right and L[left] <= pivotkey: left += 1 L[right] = L[left] L[left] = pivotkey return left
以一趟排序为例[5, 9, 1, 11, 6, 7, 2, 4]:
-
开始排序时,left=0,right=7,首先用表的第一个下标值作为 分组关键字pivot,
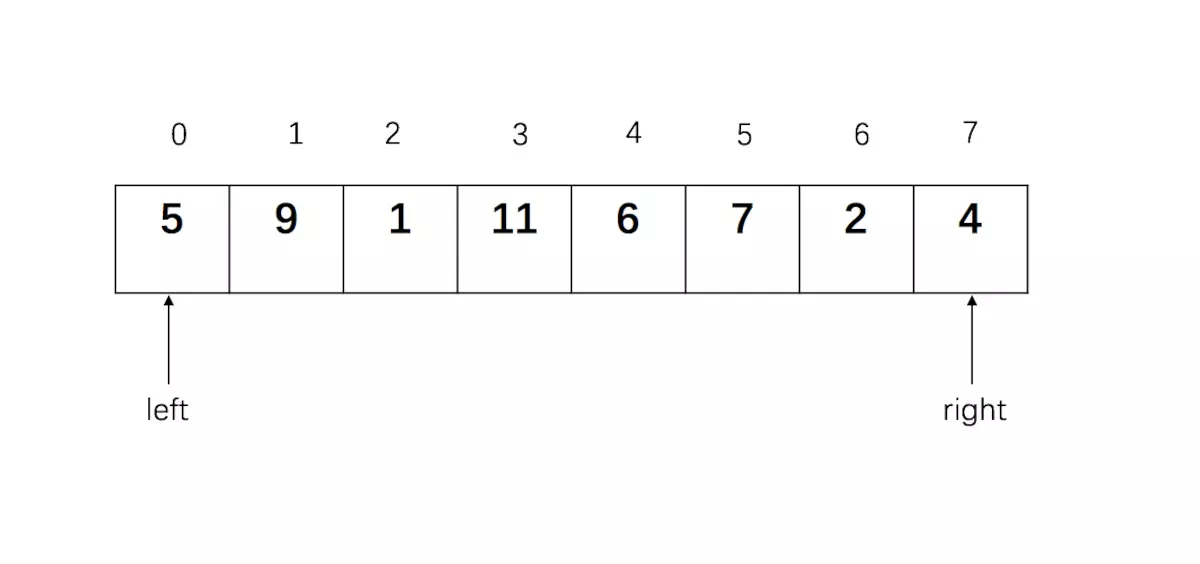
第一趟排序过程
-
进行
while left < right and L[right] >= pivotkey:判断,其中L[right]=4 不满足条件,跳出循环,执行L[left] = L[right],执行后列表变成: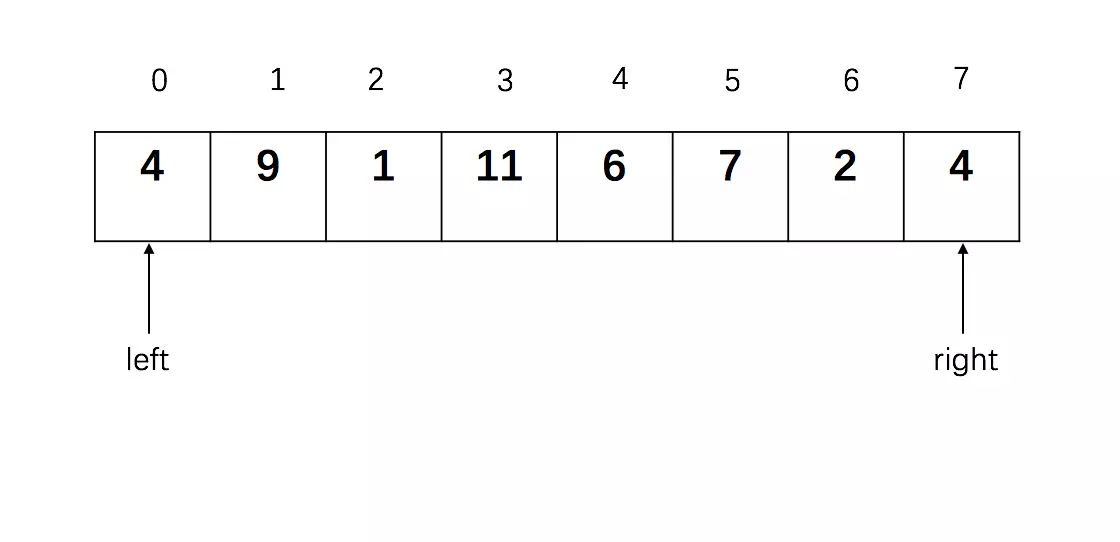
第一趟排序结果
-
然后进行
while left < right and L[left] <= pivotkey:,L[left] = 4 <= 5,条件成立,left向右边移动,然后L[left] = 9 不满足条件,执行L[right] = L[left],执行后列表变为: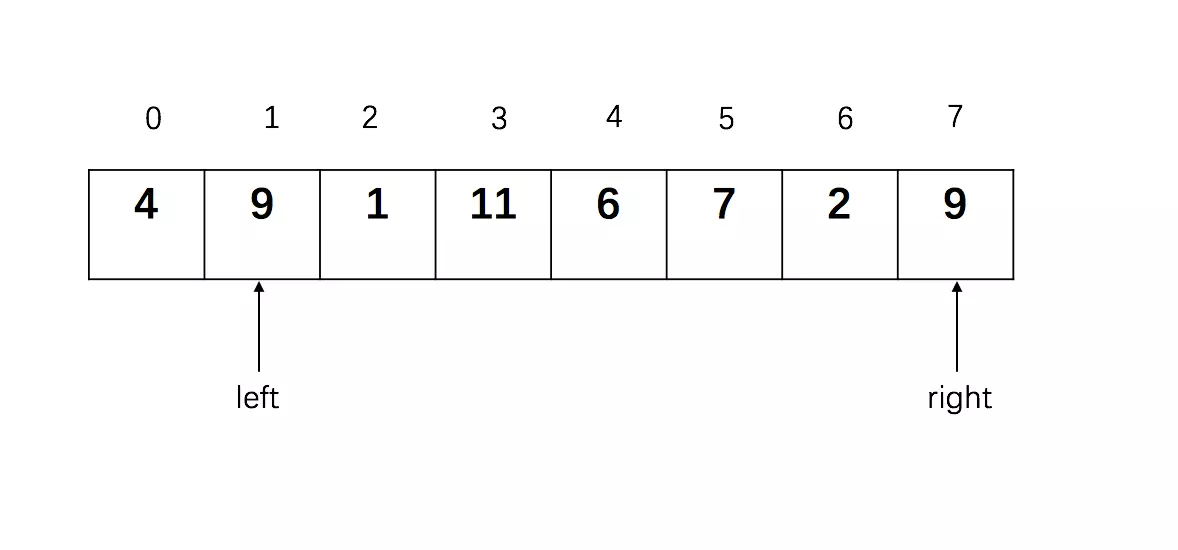
第一趟排序过程
-
然后进行
while left < right判断,条件成立,继续进行判断while left < right and L[right] >= pivotkey:,L[right] = 9,满足条件,right向左移动1,继续判断,不满足条件,执行L[left] = L[right],执行后列表变为: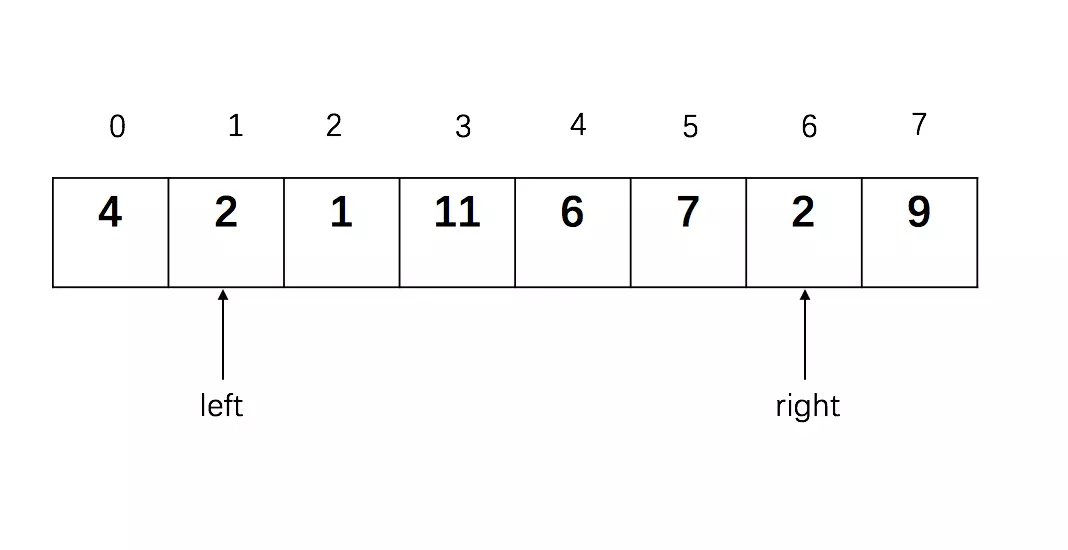
第一趟排序过程
-
然后进行
while left < right and L[left] <= pivotkey:判断,L[left] = 2,满足条件,left向右移动,然后L[left] = 1,满足条件,left向右移动,L[left] = 11,不满足条件,执行L[right] = L[left],执行后列表变为: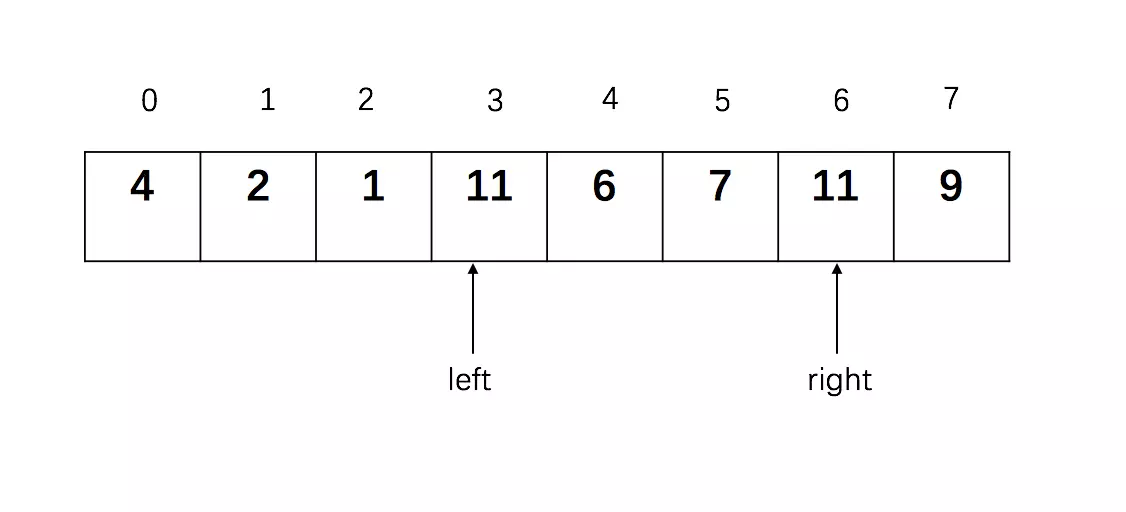
第一趟排序过程
-
然后进行
while left < right判断,条件成立,继续进行判断:while left < right and L[right] >= pivotkey:,满足条件,right向左移动,一直移动到这样的状态: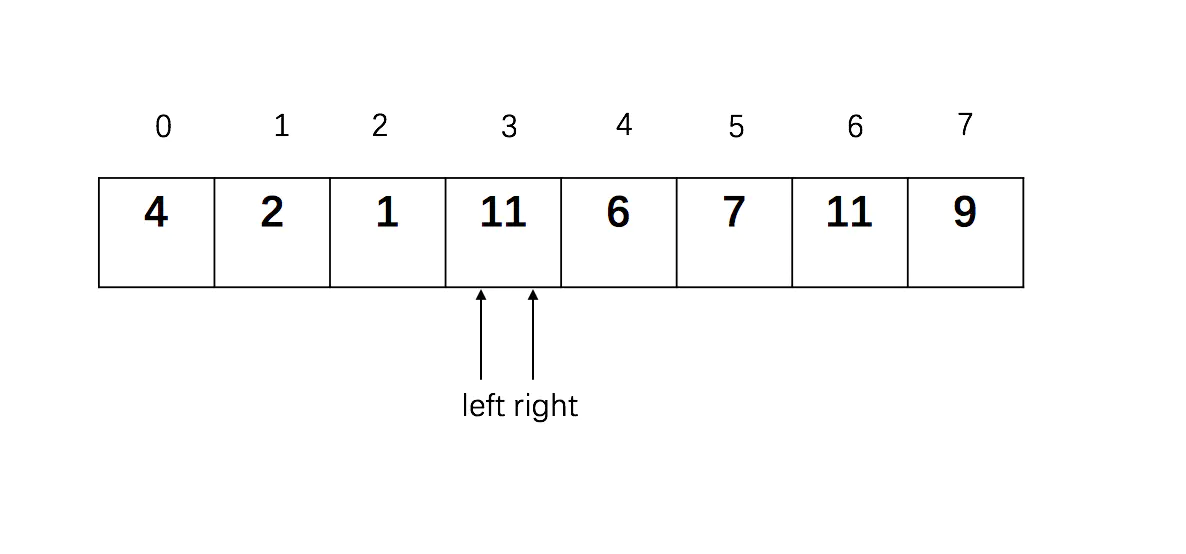
第一趟排序过程
此时不满足条件:
left < right,跳出循环。然后执行L[left] = pivotkey,并返回left下标值。此时序列变为:
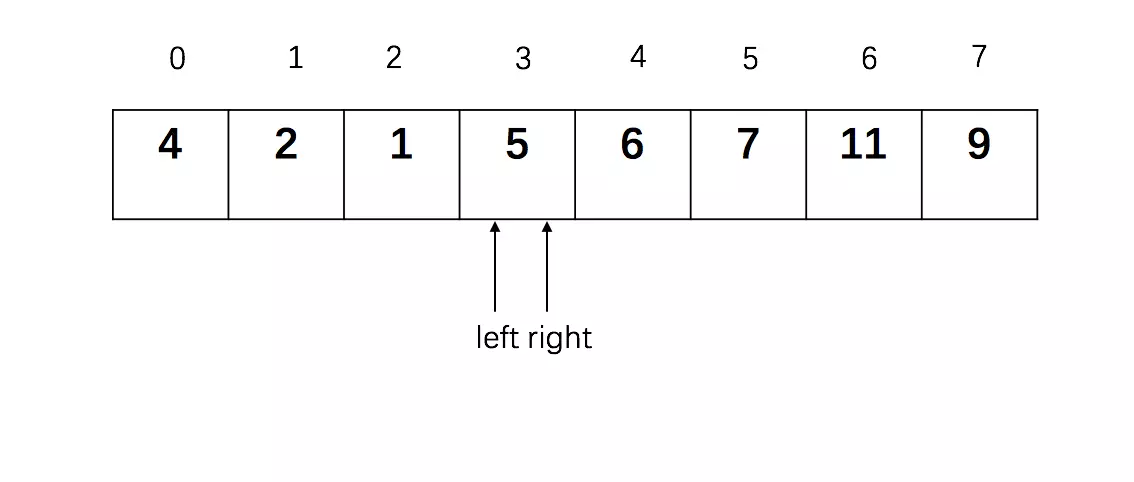
-
第一趟排序结果
接下来就是用递归分别对子列表进行排序。读者可以自己试试。
问题的优化
-
分组基准
对于上面的代码,分组基准的选取只是取列表的第一个值,太过于随便,当取到序列的中间值时,快排效率是最高的,第一个值未必是列表的中间值。为了解决这个问题,我们可以选取列表中的几个值进行简单的比较,然后取这几个值的中间值 作为分组基准。 这里就不写代码了,读者可以自己实现。 -
空间使用大。
上面的代码已经解决了比较次数的问题。 -
若序列长度过于小(比如只有几个元素),快排效率就不如插入排序了。
我们可以设置一个列表元素大小的临界值,若小于这个值,就用插入排序,大于这个值用快排。
链接:https://www.jianshu.com/p/2b2f1f79984e
–
–
 江哥架构师笔记
江哥架构师笔记
评论前必须登录!
注册